Hệ thập phân đến Hệ cơ sở khác
Các bước thực hiện
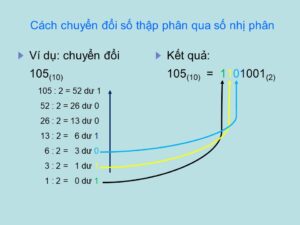
Bước 1 – Chia số thập phân được chuyển đổi cho giá trị của cơ số mới.
Bước 2 – Lấy phần còn lại từ Bước 1 là chữ số tận cùng bên phải (chữ số có nghĩa nhỏ nhất) của số cơ sở mới.
Bước 3 – Chia thương của lần chia trước cho cơ số mới.
Bước 4 – Ghi phần còn lại từ Bước 3 dưới dạng chữ số tiếp theo (bên trái) của số cơ sở mới.
Lặp lại các Bước 3 và 4, lấy các phần còn lại từ phải sang trái, cho đến khi thương số trở thành 0 ở Bước 3.
Phần còn lại cuối cùng do đó thu được sẽ là Chữ số quan trọng nhất (MSD) của số cơ sở mới.
Ví dụ :
Số thập phân: 2910
Chuyển đổi qua hệ thống số nhị phân
Bước | Hoạt động | Kết quả | Phần còn lại |
| Bước 1 | 29/2 | 14 | 1 |
| Bước 2 | 14/2 | 7 | 0 |
| Bước 3 | 7/2 | 3 | 1 |
| Bước 4 | 3/2 | 1 | 1 |
| Bước 5 | 1/2 | 0 | 1 |
Trong Bước 2 và 4, phần còn lại phải được sắp xếp theo thứ tự ngược lại để phần còn lại đầu tiên trở thành Chữ số có ý nghĩa thấp nhất (LSD) và phần còn lại cuối cùng trở thành Chữ số có ý nghĩa nhất (MSD).
Số thập phân :2910 = Số nhị phân :111012 .
Hệ thống cơ sở khác đến hệ thống thập phân
Các bước
Bước 1 : Xác định giá trị cột (vị trí) của mỗi chữ số (điều này phụ thuộc vào vị trí của chữ số và cơ số của hệ thống số).
Bước 2 : Nhân các giá trị cột thu được (ở Bước 1) với các chữ số trong các cột tương ứng.
Bước 3 : Tính tổng các số được tính ở Bước 2. Tổng là giá trị tương đương dưới dạng thập phân.
Ví dụ : Số nhị phân 111012
Các bước chuyển đổi
Bước | Số nhị phân | Số thập phân |
| Bước 1 | 111012 | ((1 × 24 ) + (1 × 23 ) + (1 × 22 ) + (0 × 21 ) + (1 × 20 ))10 |
| Bước 2 | 111012 | (16 + 8 + 4 + 0 + 1)10 |
| Bước 3 | 111012 | 2910 |
Số nhị phân :111012 = Số thập phân 2910

Chuyển đổi số nhị phân qua thập phân
Bài tập số 1:
Hãy chuyển đổi các số sau đây ra số nhị phân:2,4,8,16,32,64,128,256,192,168,1,255
Đáp án:
| Số thập phân | Số nhị phân |
|---|---|
| 1 | 00000001 |
| 2 | 00000010 |
| 4 | 00000100 |
| 8 | 00001000 |
| 16 | 00010000 |
| 32 | 00100000 |
| 64 | 01000000 |
| 128 | 10000000 |
| 192 | 11000000 |
| 168 | 10101000 |
| 255 | 11111111 |
| 256 | 100000000 |
📌 Lưu ý:
Các số nhị phân được biểu diễn với 8 bit (1 byte) trừ số 256 cần 9 bit.
Bạn có thể dùng phương pháp chia liên tiếp cho 2 để tự thực hiện chuyển đổi như đã trình bày trong bài học.
Bài tập số 2:
Hãy chuyển đổi các ký số nhị phân sau thành thập phân:
a. 1010101
b. 1111111
c. 1100111
d. 1010111
